Information

What are Fractals?

The best definition of a fractal is known as a never-ending pattern. These infinitely complex patterns are found everywhere around us and show up in much of what we see on a day to day basis. They are created by repeating a simple process over and over in an ongoing feedback loop. Driven by recursion, fractals are images of dynamic systems – the pictures of Chaos. Geometrically, they exist in between our familiar dimensions. Fractal patterns are extremely familiar, since nature is full of fractals. For instance: trees, rivers, coastlines, mountains, clouds, seashells, hurricanes, etc. Abstract fractals – such as the Mandelbrot Set – can be generated by a computer calculating a simple equation over and over.

These equations are shown within this project and described through C++ algorithms.

Sierpinski’s Carpet

Along with the triangle these are two of the most well known fractal designs.

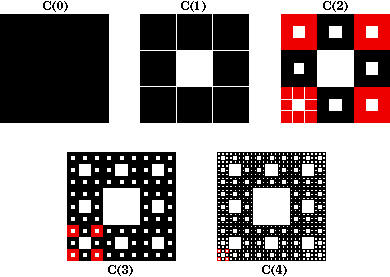
Start with a solid (filled) square C(0). Divide this into 9 smaller congruent squares. Remove the interior of the center square (that is, do not remove the boundary) to get C(1). Now subdivide each of the eight remaining solid squares into 9 congruent squares and remove the center square from each to obtain C(2). Continue to repeat the construction to obtain a decreasing sequence of sets.

The Sierpinski carpet is the intersection of all the sets in this sequence, that is, the set of points that remain after this construction is repeated infinitely often. The figures below show the first four iterations. The squares in red denote some of the smaller congruent squares used in the construction.

Special Properties

Suppose the area of the original square C(0) is equal to 1. To get C(k+1), we scale C(k) by 1/3, which reduces the area by 1/9 = (1/3)2. But we make 8 copies of this scaled version to form C(k+1). Therefore the area of C(k+1) must be (8/9)th of the area of C(k). This means that the area of C(n) is (8/9)n for all n.

Notice that these areas go to 0 as n goes to infinity. This means that we have removed “all” of the area of the original square in constructing the Sierpinski carpet. But of course there are many points still left in the carpet. That is one reason why area is not a useful dimension for this set.

Sources

http://larryriddle.agnesscott.org/ifs/carpet/carpet.html http://fractalfoundation.wolfesongs.com/